第一章 导言
1.1凸包的例子
根据特性:所有点都在凸包任意边的右侧,O(n^2)
改进:上凸包和下凸包两次构建,根据X轴方向按顺序遍历 O(nlogn)
1.2退化及鲁棒性
算法建立过程的三个阶段
- 最初阶段,忽略一些退化情况,建立总体处理思路
- 第二阶段,对最初阶段设计的算法进行调整以处理退化情况/对问题的几何性质重新分析,将特例集成到一般情况中
- 最后阶段,具体的实现,逐一实现基本操作
注意鲁棒性,主要关注浮点计算带来的误差
第二章 专题图叠合
2.1线段求交
遍历判断,O(n^2)
通过投影,排除不可能相交的线段,即按y轴平面扫描算法,将端点和交点作为事件点,更新状态结构后判断新引入线段与左右线段是否相交
算法考虑点:
上端点,交点,下断点事件的处理
水平线段的处理(重写比较大小函数)
状态结构的实现(平衡二分查找树)
特殊情况:多线段交于一点
2.2双向链接边表
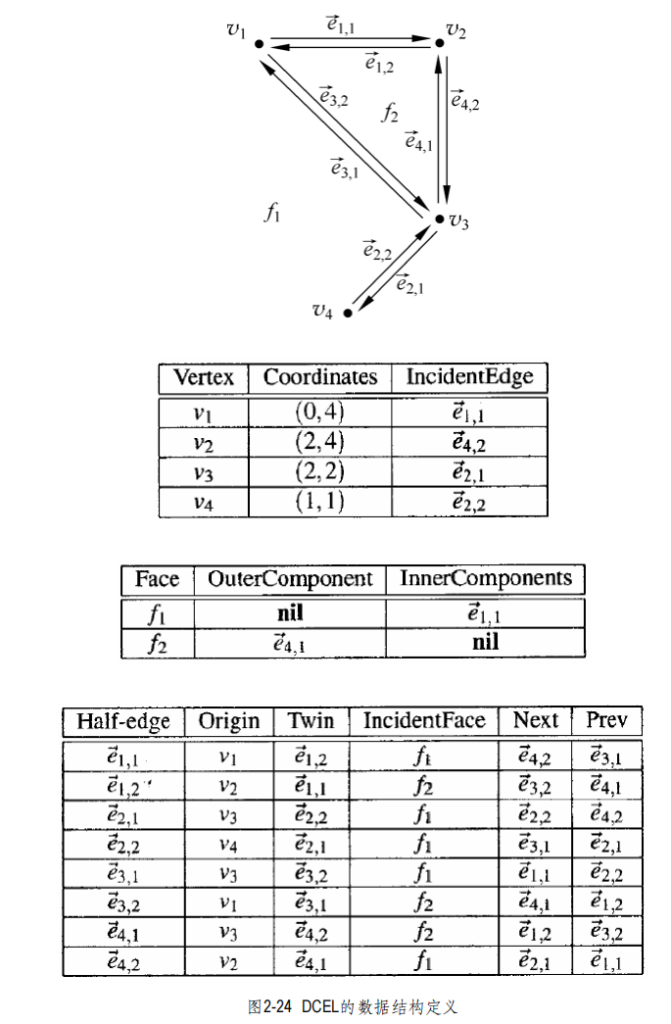
子区域划分的表示方法,首先一种简单的表示方法,即双向链接边表,能实现:围绕某张面(多边形)遍历一周,在指定一条公共边之后,通过与其相邻一侧的面,找到另一侧的那张面;在给定一个顶点之后,(依次)枚举出与之关联的所有边。
对任一子区域的划分,与之对应的双向链接边表为其中的每张面,每条边和每个顶点都设置了一个记录,不仅存有几何、拓扑信息,还有一些附加信息(属性信息)。
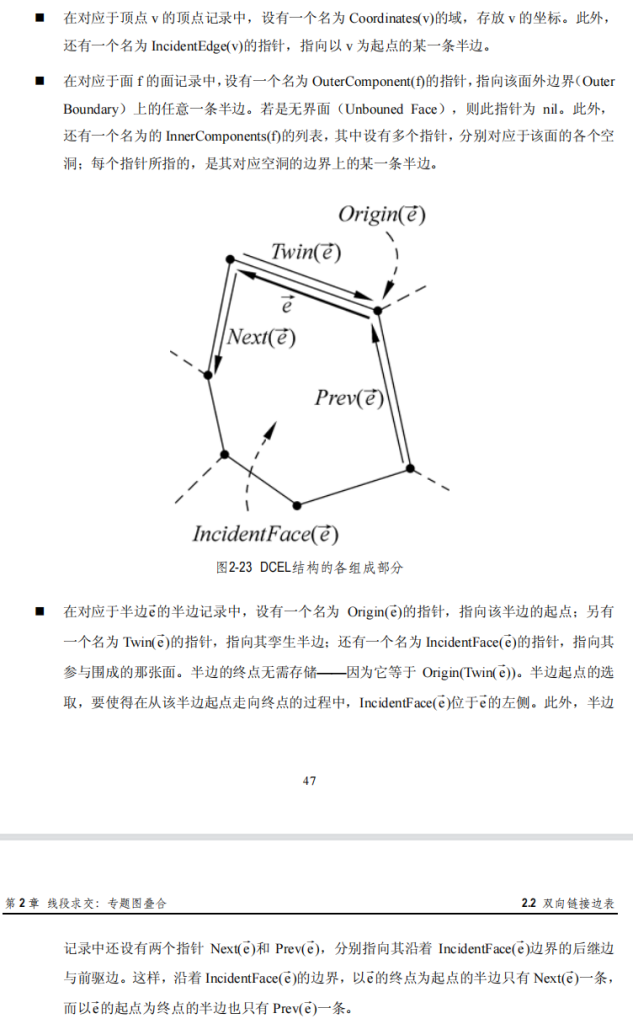
孪生半边,将一条边拆为两个半边,半边具有方向,这样,任意一条半边都有唯一的后继半边,前驱半边,半边围成的面一定在其左侧(逆时针遍历)。
但是在有空洞的情况下,按逆时针遍历,面却在右侧。所以定义空洞按顺时针遍历。
2.3计算子区域划分的叠合
所谓叠合,就是由来自S1和S2的边共同在平面上导出的一个子区域划分。我的理解就是求出所有交点,更新所有边(旧边可能被分成多个新边)以及对应的双向链接边表。
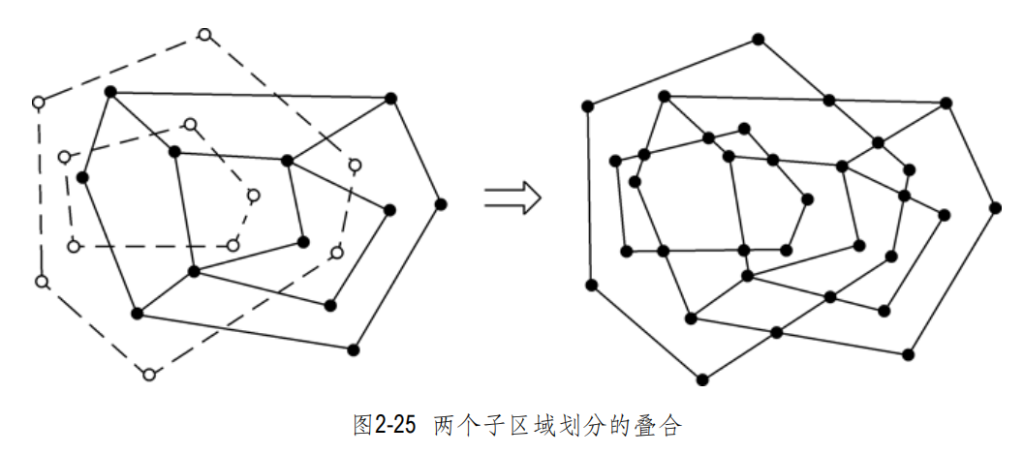
分析一下可以知道,旧子区域划分中的一部分边是没有相交的,这些未受影响的半边记录可以继续沿用。而相交的半边信息需要更新。因此应将S1,S2对应的两个双向链接边表复制到一个新的双向链接边表中,计算交点,将相关部分链接。除此之外,新增面的计算显然更加复杂。
算法实现需要 1存放事件点的事件队列 2状态结构(平衡二分查找树,记录与当前扫描线相交的所有线段)3双向链接边表,初始状态为S1和S2双向链接边表的拷贝
像上节计算交点一样从上向下扫描,到端点时进行判断,如果端点有关的边都来自于一个子区域划分,则不需要更新,跳过。否则需要更新该交点有关的边。普通交点,即两条边相交,就将一条边的两个半边保留不动(因为出发点没变),然后新增两个以交点为出发点的相反的两条半边作为原来两个边的twin边即可,同样处理另一条原始边。之后更新这些半边的prev和next边信息,按一个方向转着一组一组链接就行。特殊情况要考虑边穿过另一子区域端点的情况。
更新完端点和边后再去遍历边界环去更新面信息,注意外边界和空洞边界的判断区分,检查最左边点前后边的旋转角度即可。另外一张面可能有多条边界(空洞的存在),需要构建图结构来判断。

2.4布尔运算
布尔运算算是GIS软件里最基础的功能了。
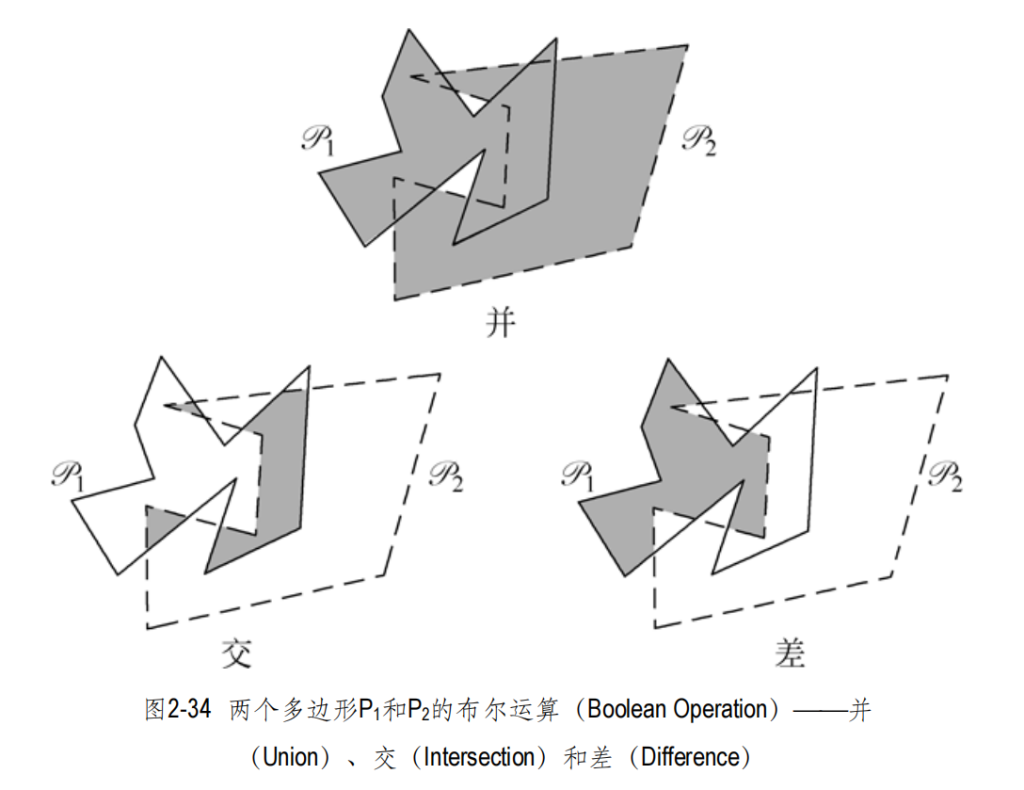
布尔运算只需要在叠合计算上加一个标记即可,在边界面先做好标记P1,P2,再按实际的布尔运算(交,并,差)提取相应的面即可。
第三章 多边形三角剖分
3.1看守与三角剖分
通过极大的一组互不相交的对角线,可以将一个多边形分解为多个三角形⎯⎯ 我们称之为该多边形的一个三角剖分(Triangulation)
定理 3-1 任何简单多边形都存在(至少)一个三角剖分;若其顶点数目为 n,则它的每个三角剖分 都恰好包含 n - 2 个三角形。
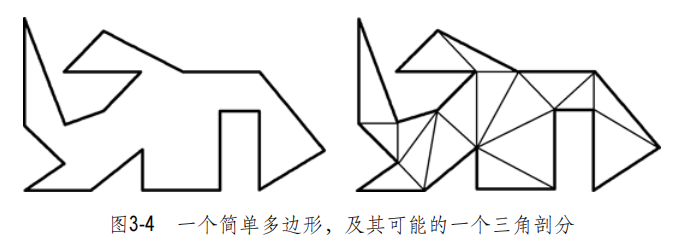
定理证明:类似递归,对当前多边形最左边的点周围两点连线,得到对角线,并考虑特殊情况。
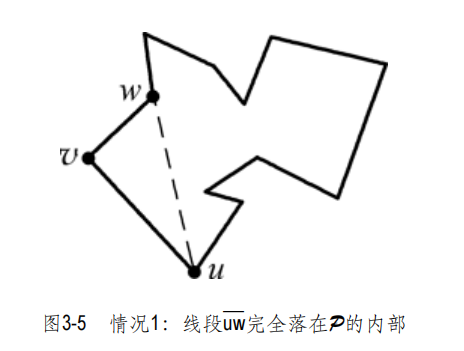
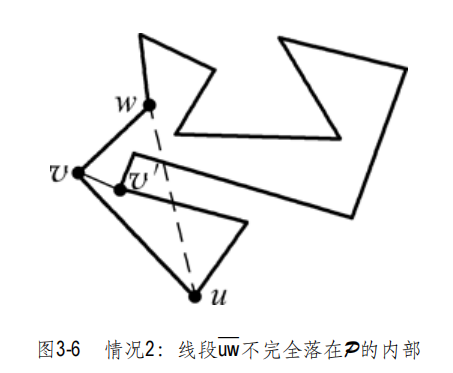
特殊情况处理:在所有这些顶点中,令v'为与—uw相距最远 者。现在,联接v'和v的那条(开)线段,不可能与P的任何边相交⎯⎯否则,这条边的两 个端点中,必有其一会落在这个三角形内部,而且该端点到—uw的距离要比v'更远。因此, —vv'就是一条对角线。
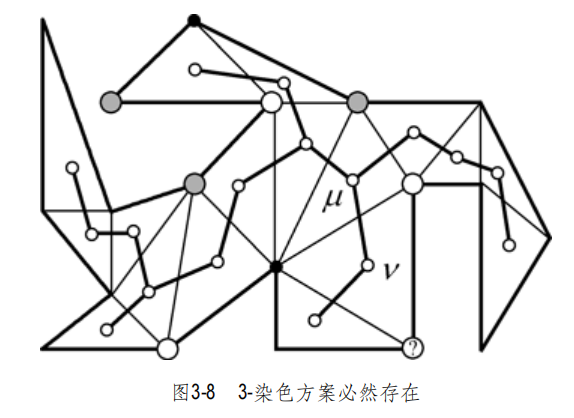
剖分后进行三染色处理,选用点数最少的那一类同色顶点,并为它们配备摄像机,则只需不超过n/3台摄像机,即可覆盖住P。
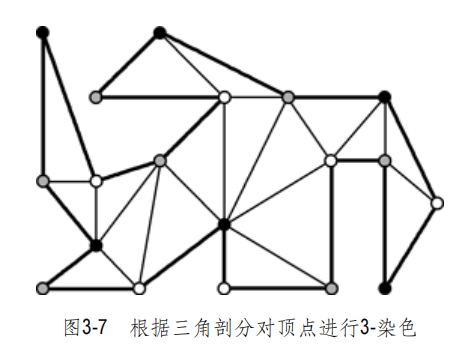
三染色可以通过DFS等遍历方法计算。三角剖分的每个三角形对应点连线,构成网络,遍历即可。
3.2 多边形的单调块划分
如果按照多边形存在三角剖分的证明过程来实现三角剖分,考虑到证明过程中存在的特殊情况(最左顶点的相邻两点连线不完全包含在多边形内),那么复杂度是O(n^2)。优化方法是将多边形先分成单调块。
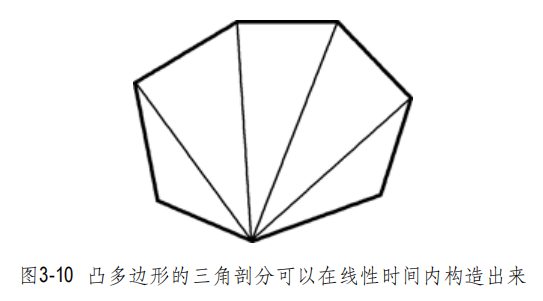
显而易见,凸多边形的三角剖分不存在上述特殊情况,因此可以从左到右依次剖分。然而不幸的是,将多边形划分为凸块的难度,与对它做三角剖分是一样的。因此,我们将 把P划分为所谓的“单调块”(Monotone Piece)⎯⎯这项工作要容易得多。
我们称一个简单多边形“关于某条直线 l 单调”(Monotone with respect to a line l),如果对任何一条垂直于 l 的直线 l',l'与该多边形的交都是连通的。换而言之,它们的交或者是一条线段,或者是一个点,也可能是空集。
好理解一点的特性是:在沿着多边形的左(右)边界,从最高顶点走向最低顶点的过程中,我们始终都是朝下方(或者水平)运动,而绝不会向上。
将多边形划分为单调块的方法:简单来说就是引入对角线消除拐点。具体操作无非是对分裂/汇合顶点的分情况讨论。(略)
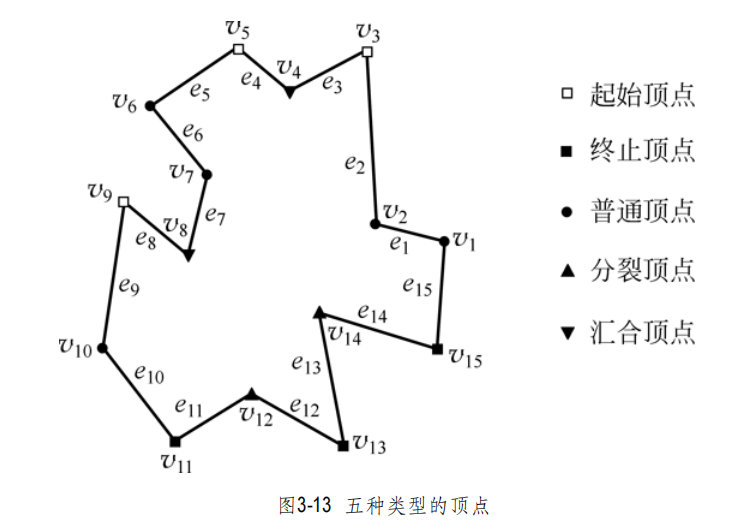
3.3 单调多边形的三角剖分
划分为单调多边形后即可在线性时间进行三角剖分。(略)
4 线性规划:铸模制造
4.1 铸造中的几何
设P为一个三维的多面体⎯⎯也就是由多张二维小平面(Facet)围成的一个三维形体⎯⎯而且,其中有一个小平面被指定为顶面。(对于多面体的概念,我们不打算给出准确而形式化的定义。这类定义过于复杂,在这里没有必要。)我们假定,铸模的外轮廓呈立方体形状,而其内部的空洞则与P完全一致。如果将这个多面体放入到铸模中,其顶面将与铸模的顶面共面平齐⎯⎯我们假设这张平面与xy-平面平行。也就是说,若试图将P抽取出来,则在铸模的上方不会受到任何不必要部分的阻挡。
除了顶面之外,P 的其它小平面都被称作普通面(Ordinary Facet)。P 的任何一张普通面 f,都与铸模的某张小平面相对应,我们记之为^f
只通过一次平移运动,能否可以将 P 从铸模中抽取出来?我们希望对此做出判断。换而言之,我们所要判断的是:是否存在某个方向→d,使得在沿着这个方向将 P 平移至无穷远的过程中,P 与铸模体的任何部分都不会相交。需要注意的是,这里允许 P 紧贴铸模的边界运动。既然在 P 的各张小平面中,只有顶面没有和铸模接触,故移出的方向必然要朝上⎯⎯也就是说,其在 z-方向上的分量必须为正。当然,这只是移出方向应该具备的必要条件之一;关于合法的移出方向,我们还需要确定更多的限制条件。
任取P的一张普通面f。相对于铸模上与之对应的小平面^f,f可能的移出方式不外乎两种:要么与^f逐渐远离,要么紧贴^f滑动。为了更准确地表述这一限制条件,我们需要对三维空间中任意两个向量所构成的角度作出定义。我们的定义如下。考虑由这两个向量所生成的那张平面(这里假定两个向量都起自于坐标原点);在该平面上,这两个向量可以确定出两个角度(其和为 2π),其中较小的那个,被定义为这两个向量所成的角度。现在,若将f的外法矢(Outward Normal)记作→η(f),则沿着与→η(f)的夹角小于 90o 的任何方向的平移运动,都会受到^f的阻挡。因此,→d所应该具备的一个必要条件就是,相对于P的任何一张普通面的外法矢,→d与之所成的角度都必须至少是90° 。反过来,下面的这则引理将告诉我们,这个条件也是充分的。
引理 4-1 沿着某个方向→d通过一次平移,多面体 P 能够从其铸模中抽取出来,当且仅当相对于 P 的每一张普通面的外法矢,→d与之所成的角度都至少为 90°。引理4-1给出了合法移出方向d的充要条件。那么,应该如何将这些条件转换到我们用以表示方—向的这张平面上来呢?任取一张普通面的外法矢η=(ηx,ny,nz)。方向d =(dx,dy,1)与η所成的夹ny,角不小于90°,当且仅当d与η的点积非正。这样,由每一张普通面都可以导出如下形式的一个限制条件:
→ηxdx + →ηydy + ηz ≤ 0
在平面z = 1 上,这样一个不等式所描述的正好是一张半平面⎯⎯也就是在平面上位于某条直线左(或右)侧的部分。这样,上述的制造问题已经转化为平面上的一个纯粹的几何问题:给定一组半平面,若它们公共的交集非空,则从其中找出一个点;若其公共交集为空,也要能够判断出来。倘若需要制造的多面体有n张小平面,则在平面上对应的问题最多要考虑n-1 张半平面(由顶面导出的那张半平面,不必考虑)。
4.2半平面求交
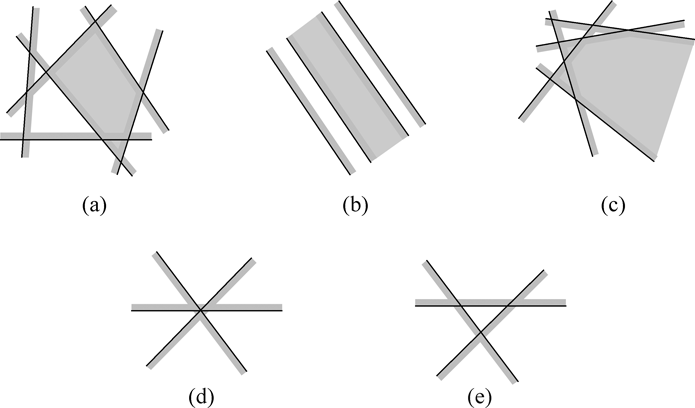
问题已经被简化为了在二维平面进行线性规划,与之前多边形求交不同,这个问题所处理的范围可能是无界的,也可能会退化成一条线段或一个点。











Comments NOTHING